Introdução à Análise de Dados para pesquisa no SUS

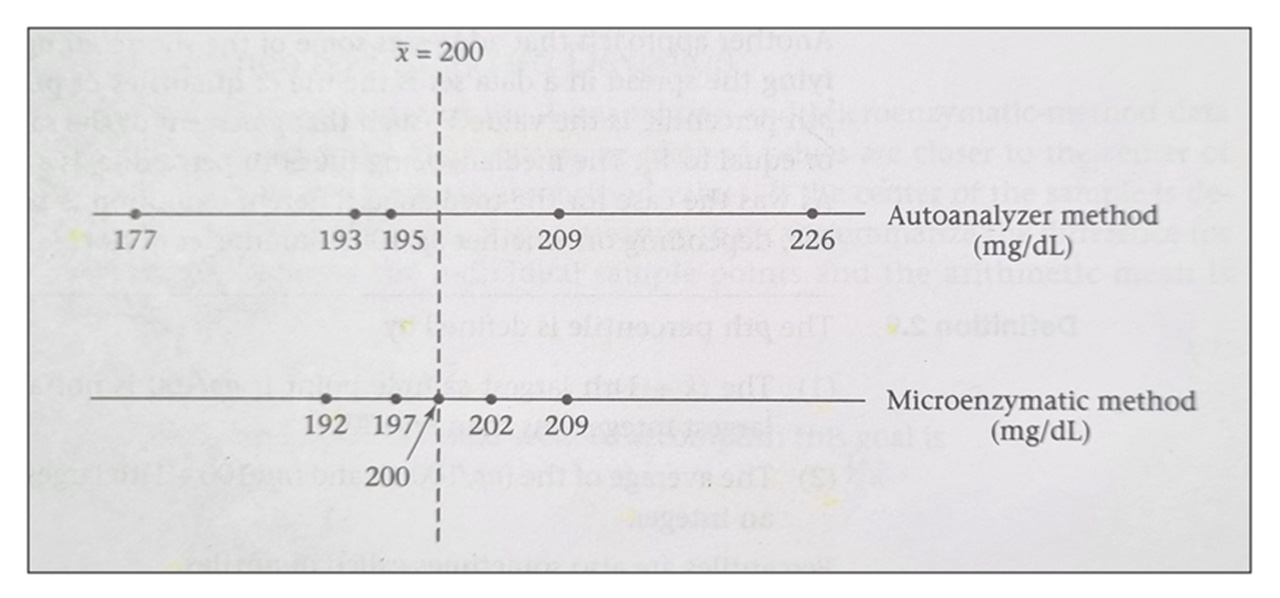
Considere as duas amostras do mesmo indivíduo apresentadas na figura a seguir, obtidas usando-se diferentes técnicas de medição. Elas têm a mesma média aritmética (200mg/dl), entretanto aparentam uma dispersão em torno da média diferente. A diferença entre as duas amostras está na variabilidade do método de medição.

Estudaremos agora diferentes estatísticas usadas para quantificar essa noção de variabilidade.

Duas amostras de medidas de colesterol usando-se os métodos AutoAnalyzer e Microenzimatic.

É a medida de variabilidade mais simples, definida pela distância entre o maior e o menor valor da amostra. Exemplo: no caso dos recém-nascidos da tabela, é dada por 2077g (4146g-2069g). Vamos pensar juntos sobre outra possibilidade de estatística para medir a dispersão dos dados.

A principal diferença entre os métodos AutoAnalyzer e Microenzimatic é a concentração dos dados ao redor do centro no segundo método. Se definirmos o centro da amostra no segundo método como sendo a média aritmética, então uma medida que poderia resumir a diferença (ou os desvios) entre os pontos individuais e a média aritmética deveria conter os termos: $(x_1-\bar{x}),(x_2-\bar{x}),...,(x_n-\bar{x})$

Sem pensar muito, uma medida simples que poderia atingir esse objetivo seria a média desses desvios: $\sum _{i=1}^n\frac{(x_i-\overline{x})}{n}$ .

Infelizmente, apesar de intuitiva, essa medida não funciona, já que, por definição, a média é construída de tal forma que a soma dos desvios das observações individuais de uma amostra em relação à média aritmética é sempre zero.

Como exercício, sugiro que você cheque essa afirmação. Vou deixar os passos indicados a seguir para ajudá-lo a chegar a essa conclusão, com base na série de colesterol aferida pelo método AutoAnalyzer:

Assim, uma alternativa é tomar o quadrado dos desvios. Dado que o quadrado de qualquer número é um número positivo, a média dos desvios ao quadrado não resultará em zero.

A estatística mais utilizada para medir o espalhamento dos dados em torno de um centro é a variância. A variância amostral é definida como a médias dos desvios ao quadrado, dividida por (n-1):

Voltando ao exemplo das duas medições de colesterol, as variâncias seriam, então:

Método AutoAnalyzer:

Método Microenzimatic:

Observe, entretanto, que a unidade da variância é o quadrado da unidade dos dados. No nosso exemplo o colesterol é medido em mg/dL — todas as medidas de locação são medidas em mg/dL e a variância em (mg/dL)².

Uma forma muito natural de “resolver” a questão de escala da variância e tornar a estatística de dispersão uma medida na mesma escala dos dados é tomando a raiz quadrada da variância. Essa “nova” estatística se chama desvio-padrão. Dessa forma, o desvio-padrão pode ser interpretado como “o quanto, em média, os dados se desviam da média”.

O desvio-padrão amostral é definido como:

Para nosso exemplo de medições de colesterol, os desvios-padrão são:

AutoAnalyzer:

Microenzimatic:

Nesse ponto, você já entendeu que a escala dos dados importa. Uma outra questão interessante a se pensar é na diferença de um desvio-padrão de 10u (unidades) em uma amostra cuja média aritmética é 10u e outra cuja média aritmética é 100u. A interpretação da concentração desses dados é completamente diferente. Enquanto na série em que $\overline{x}=10u$ , em média os dados variam também em 10u, na série $\overline{x}=100u$ , os dados variam apenas em 10u.

Dessa forma, uma estatística que relacione o desvio-padrão com a média traz uma interpretação importante sobre o quanto da média temos em desvio-padrão. Essa estatística se chama coeficiente de variação, e é definida matematicamente como sendo:

Note que o coeficiente de variação não tem unidade de medida, já que ambos (s e $\overline{x}$ ) têm a mesma unidade.

No nosso exemplo de colesterol, os coeficientes de variação para ambos os métodos são:

AutoAnalyzer:

Microenzimatic:

Olhando essa estatística a conclusão é muito mais direta: enquanto no método AutoAnalyzer o desvio-padrão representa 9,22% da média, no método Microenzimatic os dados estão bem mais concentrados, com o desvio-padrão sendo 3,14% da média.

Uma medida mais robusta para dispersão é o intervalo interquartil, uma medida menos sensível a extremos ou outliers de amplitude, uma vez que utiliza o primeiro e terceiro quartil em vez do máximo e mínimo usados no cálculo da amplitude. Matematicamente é definida como:

IQ = Q₃ - Q₁

Em que Q₁ é o valor até o qual temos 25% dos dados e Q₃ o valor até o qual temos 75% da amostra.

No nosso exemplo do colesterol essa estatística seria calculada como:

Para o método AutoAnalyzer:

Q₁: Já que (n*p)/100 não é inteiro (n=5 p=25, logo n*p/100=1,25), P₂₅ (ou Q₁) será a (k+1)-ésima maior observação, em que k é o maior inteiro menor do que (n*p)/100. Como (n*p)/100=1,25, o maior inteiro menor do que 1,25 é um, e (K+1)=2. Logo P₂₅= 2ª observação= 193mg/dL.

Q₃: Já que (n*p)/100 não é inteiro (n=5 p=75, logo n*p/100=3,75), P₇₅ (ou Q₃) será a (k+1)-ésima maior observação, em que k é o maior inteiro menor do que (n*p)/100. Como (n*p)/100=3,75, o maior inteiro menor do que 3,75 é 3, e (K+1)=4. Logo, P₇₅= 4ª observação= 209mg/dL.

Logo, IQ=Q₃-Q₁=209-193=16 mg⁄dL

Para o método Microenzimatic:

Note que, como ambas as amostras (AutoAnalyzer e Microenzimatic) têm o mesmo tamanho, Q₁ continuará sendo a 2ª observação (que agora assume o valor 197mg/dL) e Q₃ a 4ª observação da amostra (que agora é 202mg/dL).

Logo, IQ=Q₃-Q₁=202-197=5 mg⁄dL