Módulo 2 | Aula 1
Análise exploratória e descritiva
Medidas de locação
Suponha que você já coletou seus dados (primários) usando alguma das técnicas de amostragem apresentadas anteriormente, ou está usando dados secundários. Você já tem seus dados em mãos, parabéns! Agora você deve estar se perguntando como começar a explorar esses dados, ou, em outras palavras, quais inferências ou conclusões podem advir sobre essa amostra?
Para entender melhor as características dessa população, precisamos resumir o máximo possível esses dados, já que, por mais bem tabulados que eles estejam, é impossível se extrair informação de uma lista grande de números/características.
Atenção! Não estamos falando de olhar uma amostra menor do que a que já temos, pois quando mais dados, melhor! Estamos falando em resumir de forma estratégica toda essa informação em algo que nos ajude a entender e tomar decisões! E é aqui que as estatísticas de locação e dispersão entram na jogada.
Um tipo de medida muito útil para o resumo dos dados é dado pelo centro, ou meio da amostra, e as estatísticas que medem esse “meio” são as médias.
Média aritmética
A média aritmética é dada pela soma de todas as observações, dividida pelo número delas. Essa média é denotada como:
Exemplo: suponha que se pretenda entender como estão os pesos de uma amostra de 20 recém-nascidos de uma maternidade de São Paulo (Tabela 1):
| Tabela 1 - Pesos de uma amostra de recém-nascidos de uma maternidade de São Paulo | ||
|---|---|---|
| Indivíduo | Peso (g) | |
| 1 | 3265 | |
| 2 | 3260 | |
| 3 | 3245 | |
| 4 | 3484 | |
| 5 | 4146 | |
| 6 | 3323 | |
| 7 | 3649 | |
| 8 | 3200 | |
| 9 | 3031 | |
| 10 | 2069 | |
| 11 | 2581 | |
| 12 | 2841 | |
| 13 | 3609 | |
| 14 | 2838 | |
| 15 | 3541 | |
| 16 | 2759 | |
| 17 | 3248 | |
| 18 | 3314 | |
| 19 | 3101 | |
| 20 | 2834 | |
Para tal, vamos começar calculando a média amostral:
A média aritmética é, em geral, uma medida de locação muito natural. Uma de suas principais limitações é sua sensibilidade para valores extremos/aberrantes, já que nela se considera que todas as observações têm o mesmo peso. Na presença desses valores, essa estatística pode não ser a medida de locação mais apropriada para representar a amostra. Por exemplo, se o primeiro recém-nascido do nosso exemplo anterior fosse imputado erroneamente como 500 gramas (em vez de 3265 g), então a média aritmética cairia para 3028.65 g.
A média tem algumas propriedades interessantes que podem nos ajudar em momentos de crise, como medição sistemática errada. São elas:
- Se yi = xi + c, com i=1, ..., n e c é uma contante, então:
- Se yi = c * xi, com i=1, ..., n e c é uma constante, então:
Mediana
Uma medida de locação alternativa à tradicional média aritmética, e talvez a segunda mais popular é a mediana, definida pelo número que divide uma amostra ordenada em dois grupos de igual quantidade de observações. Dada uma amostra de n elementos ordenados (do menor para o maior) então a mediana será:
- Se n é ímpar, a mediana será o elemento do meio, ou o ésimo valor.
- Se n é par, a mediana não está na amostra, e será a média das duas observações do meio da amostra, ou seja, a média entre o elemento e
A razão para existência dessas duas definições é a necessidade de se separar o grupo de números em dois subgrupos de igual quantidade de elementos.
Exemplo: para calcular a mediana dos pesos dos recém-nascidos da tabela, notemos que n é par (n=20), e os números ordenados são apresentados a seguir (Tabela 1):
| Tabela 1 - Pesos ordenados da amostra de recém-nascidos da maternidade de São Paulo | ||
|---|---|---|
| Indivíduo | Peso (g) | |
| 10 | 2069 | |
| 11 | 2581 | |
| 16 | 2759 | |
| 20 | 2834 | |
| 14 | 2838 | |
| 12 | 2841 | |
| 9 | 3031 | |
| 19 | 3101 | |
| 8 | 3200 | |
| 3 | 3245 | |
| 17 | 3248 | |
| 2 | 3260 | |
| 1 | 3265 | |
| 18 | 3314 | |
| 6 | 3323 | |
| 4 | 3484 | |
| 15 | 3541 | |
| 13 | 3609 | |
| 7 | 3649 | |
| 5 | 4146 | |
Logo, a mediana será dada pela definição B, e será a média das observações 3245 e 3248, ou seja, 3246.5g.
Note que a principal característica da mediana é sua insensibilidade para valores extremos/aberrantes. Se voltássemos ao exercício de considerar que, na verdade, o recém-nascido 1 teve seu peso imputado como de 500 g, a mediana continuaria sendo 3246.5g.
Média aritmética ponderada
Essa medida é uma modificação da média aritmética. Enquanto na média aritmética simples cada elemento tem o mesmo peso (1/n), na ponderada os elementos têm pesos distintos. Ela é muito útil em exemplos em que certos atributos valem mais do que outros, como na inferência sobre a qualidade dos serviços prestados em uma unidade de saúde, com perguntas sobre os atendentes e sobre o espaço físico. Se o espaço físico for mais difícil de modificar, pode-se atribuir nota maior às perguntas referentes ao atendimento.
A média aritmética ponderada é dada por:
Como exemplo, vamos atribuir pesos diferentes (wi) aos valores medidos dos pesos dos recém-nascidos da tabela.
| Tabela 2 - Tabela 1 com uma coluna adicional para w | ||
|---|---|---|
| Indivíduo | Peso (g) | w |
| 1 | 3265 | 22 |
| 2 | 3260 | 40 |
| 3 | 3245 | 33 |
| 4 | 3484 | 22 |
| 5 | 4146 | 5 |
| 6 | 3323 | 31 |
| 7 | 3649 | 24 |
| 8 | 3200 | 35 |
| 9 | 3031 | 48 |
| 10 | 2069 | 58 |
| 11 | 2581 | 61 |
| 12 | 2841 | 20 |
| 13 | 3609 | 45 |
| 14 | 2838 | 22 |
| 15 | 3541 | 41 |
| 16 | 2759 | 35 |
| 17 | 3248 | 36 |
| 18 | 3314 | 11 |
| 19 | 3101 | 10 |
| 20 | 2834 | 25 |
A média aritmética ponderada será, então:
Quantis
As medidas de locação vistas até agora objetivam inferir sobre o centro da distribuição dos dados via diferentes perspectivas. Já os quantis expressam medidas mais gerais de locação, não se restringindo ao centro dos dados. Eles são nomeados de forma específica de acordo com a maneira como os dados são divididos. Generalizando, o q-ésimo quantil é o valor até o qual temos q% dos pontos da amostra (ordenada). Por exemplo:
-
Percentil: quando dividem-se os dados em grupos que acumulam 1% dos dados. Exemplo: P3 denota o conjunto de dados (ordenados), até o qual temos 3% das observações.

Fonte: aprendeconalf.es | Acesso em: 20 jul. 2025 -
Decil: quando dividem-se os dados de grupos que acumulam 10% deles. Exemplo: D3 denota o conjunto de dados (ordenados) até o qual temos 30% das observações.

Fonte: aprendeconalf.es | Acesso em: 20 jul. 2025. -
Quartis: quando dividem-se os dados de grupos que acumulam 25% deles. Exemplo: Q3 denota o conjunto de dados (ordenados) até o qual temos 75% das observações.
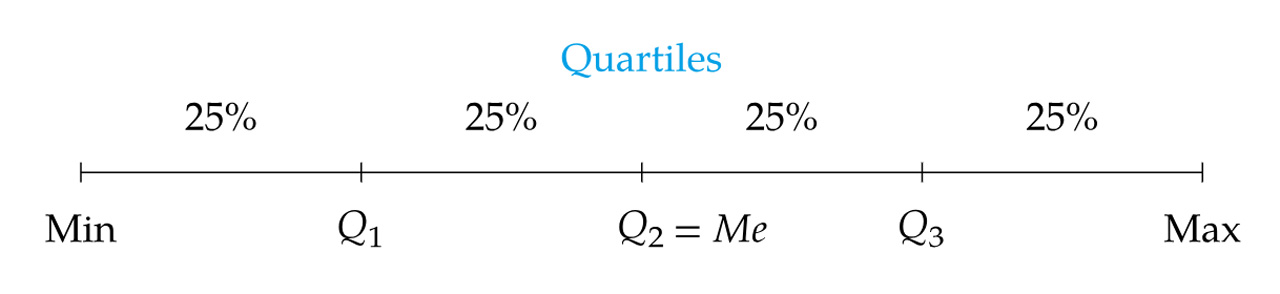
Fonte: aprendeconalf.es | Acesso em: 20 jul. 2025
Agora que já entendemos essa noção de distribuição dos dados em quantis, você já deve ter observado que a mediana é um quantil (até o qual temos 50% dos dados), assumindo os valores de P50 (quinquagésimo percentil), D5 (quinto decil) ou Q2 (segundo quartil).
Usando a definição mais fina de percentil, analogamente à mediana, obtemos essas medidas de duas formas:
- Se (n*p)/100 não for um número inteiro, o p-ésimo, percentil é a (k+1)-ésima maior observação, em que k é o maior inteiro menor do que (n*p)/100.
- Se (n*p)/100 for um número inteiro, o p-ésimo, percentil será a média entre (n*p)/100-ésima observação e a [(n*p)/100 + 1]-ésima observação.
Calma, vai fazer sentido! Vamos voltar ao exemplo do peso dos recém-nascidos. Inicialmente, precisamos que os dados estejam ordenados. Já fizemos isso para o cálculo da mediana, Tabela 1.
Então vamos supor, como exemplo, que queremos calcular o percentil 10% e 90% desses dados.
Para P10:
Já que (n*p)/100 é inteiro (n=20, p=10, logo n*p/100=2) usamos a definição (B).
Dessa forma, P10 será a média entre a 2ª e a 3ª observação: (2581+2759)/2=2670g.
Para P90:
Já que (n*p)/100 é inteiro (n=20, p=90, logo n*p/100=18) usamos a definição (B).
Dessa forma, P90 será a média entre a 18ª e a 19ª observação: (3609+3649)/2=3629g.
E quando (n*p)/100 não for inteiro? Vamos calcular P1 como exemplo:
Para P1:
Já que (n*p)/100 não é inteiro (n=20, p=1, logo n*p/100=0,2) usamos a definição (A).
Dessa forma, P1 será a (k+1)-ésima maior observação, em que k é o maior inteiro menor do que (n*p)/100. Como (n*p)/100=0,2, o maior inteiro menor do que 0,2 é zero, e (K+1)=1. Logo P1= 1ª observação= 2069g.
Faça você mesmo!
Calcule as medidas de locação no R! No script modulo2aula1_atividades.R (Atividade 2), você irá calcular média, mediana e quantis dos dados de recém-nascidos usando as funções mean(), median() e quantile() do tidyverse.
