Módulo 2 | Aula 2
Formas de visualização de dados e métodos analíticos
Introdução
A visualização de dados desempenha papel essencial na análise e comunicação de informações. Com a crescente quantidade de dados disponíveis, uma boa visualização permite que informações complexas sejam apresentadas de forma clara e compreensível.
Poderíamos simplesmente realizar as análises focando nos coeficientes, sem a necessidade de examinar gráficos com muitos pontos. Isso certamente facilitaria o processo de análise mais ágil, mas seria uma má ideia. Um dos exemplos clássicos é o quarteto de Anscombe, composto por quatro conjuntos de 11 pontos que possuem o mesmo coeficiente de correlação linear de Pearson.
| Correlação de Pearson dos conjuntos de Anscombe | ||||
|---|---|---|---|---|
| Conjunto | coeficiente | Valor de p | Limite inferior (Intervalo de confiança) | Limite superior (Intervalo de confiança) |
| 1 | 0.82 | 0.00217 | 0.424391 | 0.950693 |
| 2 | 0.82 | 0.00218 | 0.423939 | 0.95064 |
| 3 | 0.82 | 0.00218 | 0.424062 | 0.950655 |
| 4 | 0.82 | 0.00216 | 0.424639 | 0.950722 |
Agora, vamos visualizar os dados desses quatro conjuntos:
Gráfico de dispersão mostrando os quatro conjuntos de dados que formam o quarteto de Anscombe
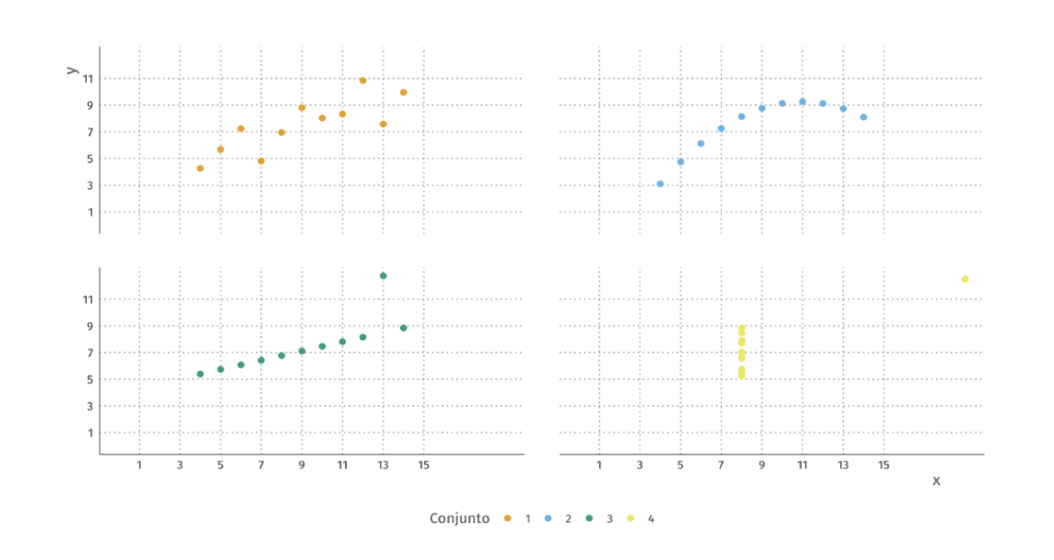
No gráfico anterior podemos ver que cada conjunto de dados tem um comportamento bem diferente. O conjunto 1 apresenta um comportamento linear, enquanto o conjunto 2 um comportamento não linear; o conjunto 3 é também linear, porém com um outlier, e o conjunto 4 apresenta um comportamento constante, porém também com outlier.
Essa possibilidade de diferentes comportamentos com mesmas métricas de sumarização foi expandido por Matejka e Fitzmaurice.
Gráfico de dispersão dos 12 conjuntos de dados propostos por Matejka e Fitzmaurice
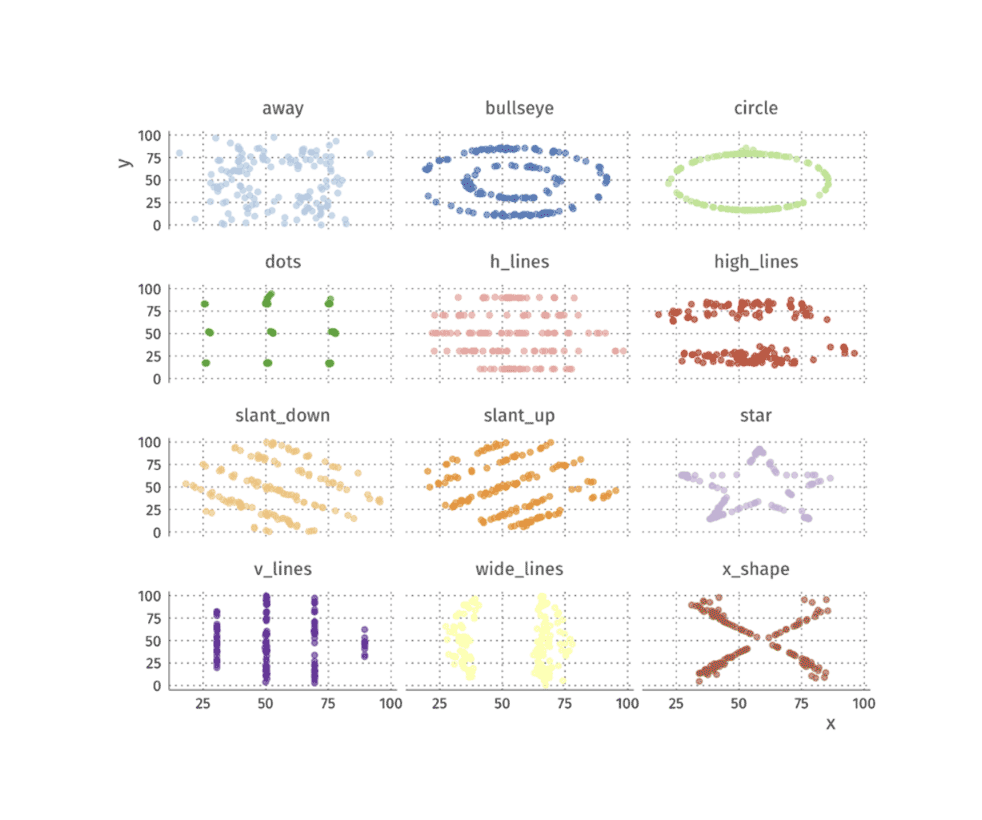
Esses 12 conjuntos de dados parecem bem diferentes, não é? Porém, vamos ver as métricas de cada um deles.
| Correlação de Pearson dos conjuntos de Anscombe | |||||
|---|---|---|---|---|---|
| Conjunto | Média X | Média Y | Desvio Padrão X | Desvio Padrão Y | Coeficiente de correlação |
| away | 54.27 | 47.83 | 16.77 | 26.94 | -0.06 |
| bullseye | 54.27 | 47.83 | 16.77 | 26.94 | -0.07 |
| circle | 54.27 | 47.84 | 16.76 | 26.93 | -0.07 |
| dots | 54.26 | 47.84 | 16.77 | 26.93 | -0.06 |
| h_lines | 54.26 | 47.83 | 16.77 | 26.94 | -0.06 |
| high_lines | 54.27 | 47.84 | 16.77 | 26.94 | -0.07 |
| slant_down | 54.27 | 47.84 | 16.77 | 26.94 | -0.07 |
| slant_up | 54.27 | 47.83 | 16.77 | 26.94 | -0.07 |
| star | 54.27 | 47.84 | 16.77 | 26.93 | -0.06 |
| v_lines | 54.27 | 47.84 | 16.77 | 26.94 | -0.07 |
| wide_lines | 54.27 | 47.83 | 16.77 | 26.94 | -0.07 |
| x_shape | 54.26 | 47.84 | 16.77 | 26.93 | -0.07 |
Como pode ser observado, os valores das métricas indicam que os conjuntos seriam muito parecidos entre si, porém o comportamento de cada um é bem diferente.
E esse exemplo pode ser extrapolado. Observe a figura a seguir. Você acreditaria que as métricas dela são semelhantes aos conjuntos mostrados anteriormente?
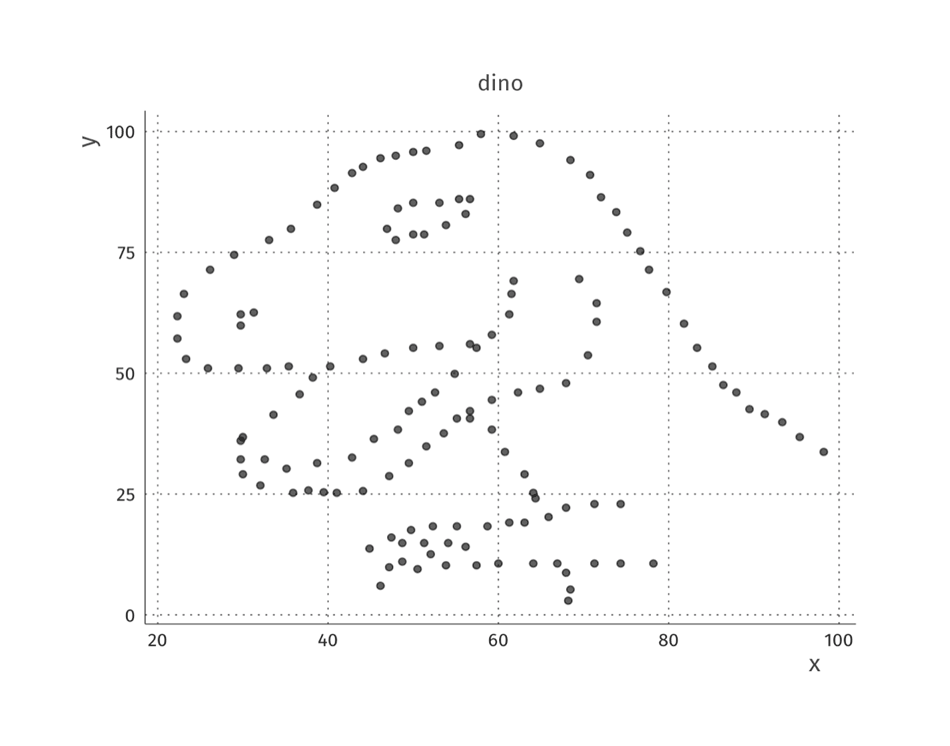
Faça você mesmo!
Explore o Quarteto de Anscombe e o Datasaurus no R! No script modulo2aula2_atividades.R (Atividades 1 e 2), você irá calcular estatísticas idênticas para conjuntos de dados completamente diferentes e visualizar por que nunca devemos confiar apenas em números.
Você pode testar conferir isso utilizando o pacote datasauRus.
Vimos a importância de visualizar os dados anteriormente à análise de dados, mas qual é a utilidade da visualização de dados após a análise?
A principal finalidade da visualização de dados é transformar os resultados de forma que seja de fácil consumo, compreensível e útil ao leitor.
Transmitir resultados por tabelas permite mostrar os dados de forma acurada e incluir muita informação, contudo tabelas não são consumidas rapidamente
Vamos ver um exemplo da diferença entre tabelas e figuras utilizando dados do artigo:
Major acute cardiovascular events after dengue infection–A population-based observational study, de Wei et. al. (2022). Nesse estudo os autores avaliaram o risco de eventos cardiovasculares após dengue.
E o que caracteriza um bom gráfico? É o que vamos descobrir!
