Módulo 1 | Aula 1
Introdução à Lógica de Programação
Iniciando a programação
Neste tópico vamos começar a entender como representar algoritmos na prática, organizando ideias de forma lógica e estruturada. A partir de exemplos simples e cotidianos, você verá como traduzir um raciocínio passo a passo em formas que podem ser entendidas por humanos e por computadores.
Para quem deseja praticar os conceitos de lógica de programação de forma visual e em português, uma boa opção é o VisualG.
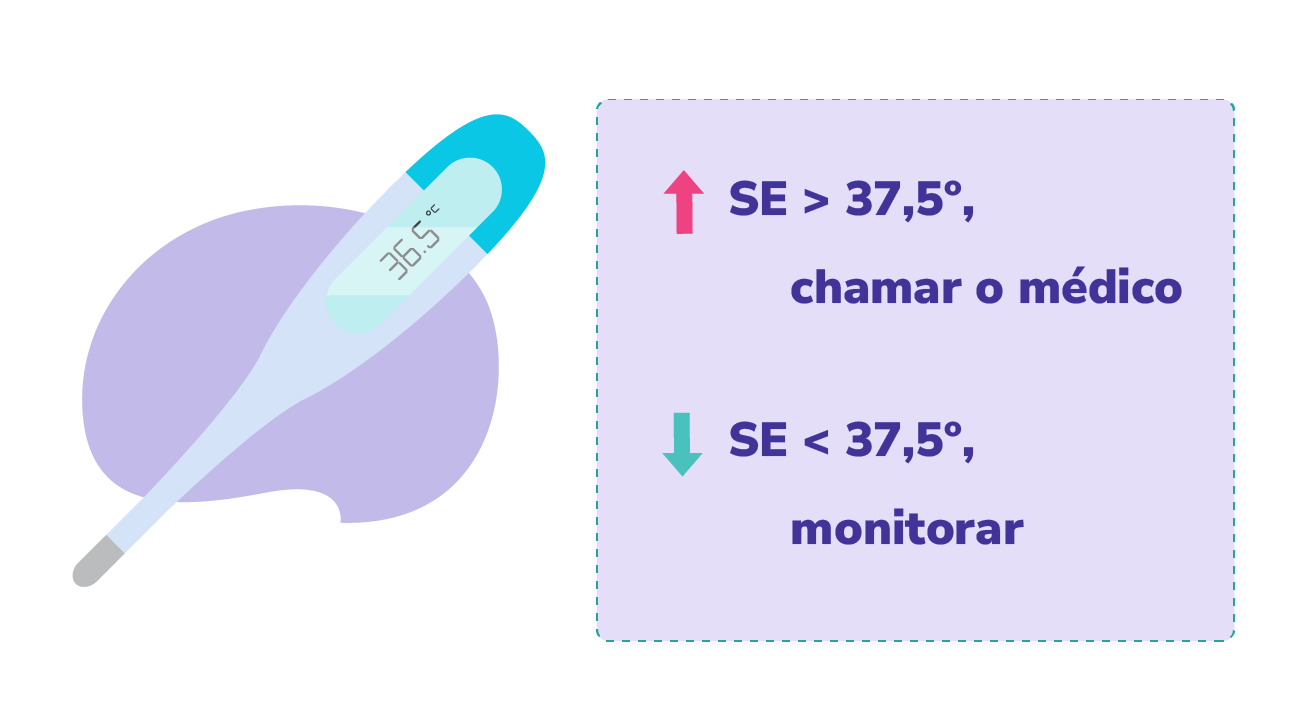
Para facilitar a compreensão das diferentes formas de representação de um algoritmo, vamos considerar um exemplo simples relacionado à área de saúde. Suponha que o algoritmo descreva o procedimento para medir a temperatura de um paciente e tomar uma decisão com base no resultado. A seguir, temos uma figura que mostra como esse algoritmo pode ser representado de três formas: em instruções passo a passo (como uma receita), em um fluxograma e em pseudocódigo usando Portugol. Esse exemplo ilustra como diferentes abordagens podem ser usadas para descrever a mesma lógica, adaptando-se às necessidades e ao público-alvo.
Informações e instruções
Em um programa de computador, lidamos essencialmente com dois elementos principais: as informações e as instruções. As informações representam os dados que o programa manipula — como números, textos ou medições —, enquanto as instruções definem o que o programa deve fazer com esses dados, como calcular, comparar ou exibir resultados. Agora, à medida que avançamos, vamos explorar como essas informações podem ser organizadas em objetos — estruturas que agrupam dados e comportamentos relacionados — e como os comandos permitem que o programa execute ações específicas. Juntos, esses conceitos são fundamentais para construir programas mais sofisticados e funcionais.
Variáveis e tipos de dados
A variável é um espaço na memória do computador que tem um endereço atribuído a um nome, no nosso contexto, durante a criação de um algoritmo. Todo objeto armazenado na memória do computador precisa ser identificado previamente. Uma variável também precisa de um tipo de dado para que seja possível realizar seu armazenamento adequado.

Suponha que a memória do computador é um armário com muitas gavetas, sendo que cada gaveta é identificada com um nome. Cada gaveta seria uma variável e, dentro da gaveta, temos um valor que queremos guardar, então podemos acessar a qualquer momento a variável desejada. O nosso armário possui gavetas de tamanhos diferentes. Algumas delas são pequenas, ideais para guardar acessórios como anéis e brincos. Outras são maiores, perfeitas para armazenar roupas. Se tentássemos colocar uma peça de roupa em uma gaveta destinada a acessórios, ela não caberia. Por outro lado, se colocássemos um pequeno acessório em uma gaveta grande, estaríamos desperdiçando espaço. Isso é semelhante ao conceito de variáveis e tipos de dados em programação. Cada tipo de dado precisa ser armazenado em uma “gaveta” (ou variável) de tamanho apropriado, caso contrário podemos ter problemas de espaço ou eficiência.
Existem alguns tipos de dados básicos ou primitivos.
pan_tool_alt CliqueToque e arraste os cards para conhecê-los.
Um problema comum relacionado aos tipos de dados é guardar números inteiros em variáveis do tipo caracter. Embora isso funcione, perdemos eficiência. Já no caso inverso, tentar armazenar um nome como “saúde” em uma variável do tipo inteiro resultaria em um erro ou na alteração do tipo para caracter a depender da linguagem de programação, como veremos ainda neste curso.
Em algumas linguagens de programação, é necessário especificar o tipo da variável no momento de sua criação, enquanto outras realizam a tipagem automaticamente com base no valor atribuído.
Sintaxe
// Declaração de variável com tipo especificado
Inteiro idade
idade = 18
// Sem especificar tipo (quando não é obrigatório)
idade = 18
No exemplo anterior a variável idade fica com o tipo inteiro, se o valor fosse 18.5 o tipo seria real, se o valor fosse "18A", seria do tipo string (ou caracter).
Operadores aritméticos
Operadores aritméticos são aqueles que permitem a realização de cálculos matemáticos de um algoritmo, exceto o operador de atribuição (=) que pode ser usado também para processamento lógico. Os operadores aritméticos são categorizados de duas formas: binários ou unários.
São binários quando utilizados em operações como radiciação, exponenciação, divisão, multiplicação, adição e subtração.
São unários quando usados para inverter um valor numérico, de positivo para negativo ou o inverso.
A tabela a seguir apresenta os operadores aritméticos a serem utilizados na construção de expressões aritméticas. Observe que existe prioridade de execução dessas operações que serão executadas. Assim, caso seja necessário alterar a prioridade de execução, é preciso utilizar parênteses.
| Tabela de operadores aritméticos | |||||
|---|---|---|---|---|---|
| Operador | Operação | Descrição | Tipo | Prioridade | Resultado |
| + | "+n" ou "n" | Manutenção de sinal | Unário | - | Positivo |
| - | -n | Inversão de sinal | Unário | - | Negativo |
| ← | x ← n | Atribuição do valor “n” a “x” | Binário | - | Positivo ou Negativo |
| ↑ | x ↑ n | Exponenciação de xⁿ | Binário | 1 | Inteiro ou Real |
| ↑ (1 / n) | x ↑ (1 / n) | Radiciação de ⁿ√x | Binário | 1 | Real |
| / | x / n | Divisão de “x” por “n” | Binário | 2 | Real |
| * | x * n | Multiplicação de “x” por “n” | Binário | 2 | Inteiro ou Real |
| + | x + n | Adição de “x” com “n” | Binário | 3 | Inteiro ou Real |
| − | x − n | Subtração de “n” de “x” | Binário | 3 | Inteiro ou Real |
| div | x div n | Divisão de “x” por “n” | Binário | 4 | Inteiro |
A tabela apresenta os operadores segundo a ordem de prioridade matemática em que as operações são realizadas, exceção à definição do operador div, que é aritmético e de uso exclusivo para obtenção de quocientes inteiros e, por esta razão, possui nível de prioridade inferior a qualquer outro operador aritmético.Caso necessite alterar o nível de prioridade de um referido cálculo, ele deve ser colocado entre parênteses. Na abordagem computacional não se utilizam chaves ou colchetes, normalmente usados na área matemática.
Fonte: Oliveira; Garcia (2016, p. 47).